选自:这里。今天忙里偷闲上了下 TeX Stack Exchange,看到一个很赞的帖子,问题的作者应该是个老师,想通过 TikZ 画导数的推导过程,也就是一个动画的过程,坛子上的达人给出了很优秀的回答,有 TikZ\PStricks\MP等等方法,本文选取了 TikZ 的实现方式,供网友学习!
代码展示
%!TEX program = pdflatex
\documentclass{standalone}
\usepackage{mathpazo}
\usepackage{tikz}
\usetikzlibrary{arrows,intersections}
\begin{document}
% TikZ 设定
\tikzset{thick,
>=stealth',
dot/.style={draw,fill=white,circle,inner sep=0pt,minimum size=4pt}
}
\begin{tikzpicture}
% 画坐标系 并且定义了 O 、xmax 和 ymax
\coordinate (O) at (0,0);
\draw[->] (-0.3,0) -- (8,0) coordinate[label={below:$x$}] (xmax);
\draw[->] (0,-0.3) -- (0,5) coordinate[label={right:$f(x)$}] (ymax);
% 给出直线 x 与曲线 y 的路径
\path[name path=x] (0.3,0.5) -- (6.7,4.7);
\path[name path=y] plot[smooth] coordinates {(-0.3,2) (2,1.5) (4,2.8) (6,5)};
% 利用 intersections 包的计算方法,得到了直线与曲线的交点坐标,分别命名为 i-1 和 i-2 (图中分别为 P 和 Q) 过点 P 的水平线与过 Q 的竖直延长线的交点标记为 M.
\begin{scope}[name intersections = {of= x and y,name = i}]
% 将PQ所形成的三角形区域(PQM)填充为灰色
\fill[gray!20] (i-1) -- (i-2 |- i-1) -- (i-2) -- cycle;
% 在空白处标记 Sekante
\draw (0.3,0.5) -- (6.7,4.7) node[pos=0.8,below right] {Sekante};
% 画出曲线路径 y,与之前代码几乎一样
\draw[red] plot[smooth] coordinates {(-0.3,2) (2,1.5) (4,2.8) (6,5)};
% 从 P 向 x 轴引垂线,垂足坐标为 (i-1 |- O),标签为 x_0
\draw (i-1) node[dot,label={above:$P$}] (i-1) {} -- node[left] {$f(x_0)$} (i-1 |- O) node[dot,label={below:$x_0$}] {};
% Q 点向 M 引垂线
\path (i-2) node[dot,label={above:$Q$}] (i-2) {} -- (i-2 |- i-1) node[dot,label={right:$M$}] (i-12) {};
% M 向 x 轴引垂线,并且标注
\draw (i-12) -- (i-12 |- O) node[dot,label={below:$x_0 + \varepsilon$}] {};
% 连接 Q 与 M,并且标注
\draw[blue,<->] (i-2) -- node[right] {$f(x_0 + \varepsilon) - f(x_0)$} (i-12);
% 连接 P 与 M
\draw[blue,<->] (i-1) -- node[below] {$\varepsilon$} (i-12);
% x 轴上两个垂足之间标记
\path (i-1 |- O) -- node[below] {$\varepsilon$} (i-2 |- O);
% Q 的水平延长线
\draw[gray] (i-2) -- (i-2 -| xmax);
% 标注 Q 点的垂直距离,最精彩的是用到了 xshift=-0.5cm,简直赞!
\draw[gray,<->] ([xshift=-0.5cm]i-2 -| xmax) -- node[fill=white] {$f(x_0 + \varepsilon)$} ([xshift=-0.5cm]xmax);
\end{scope}
\end{tikzpicture}
\end{document}
效果图:
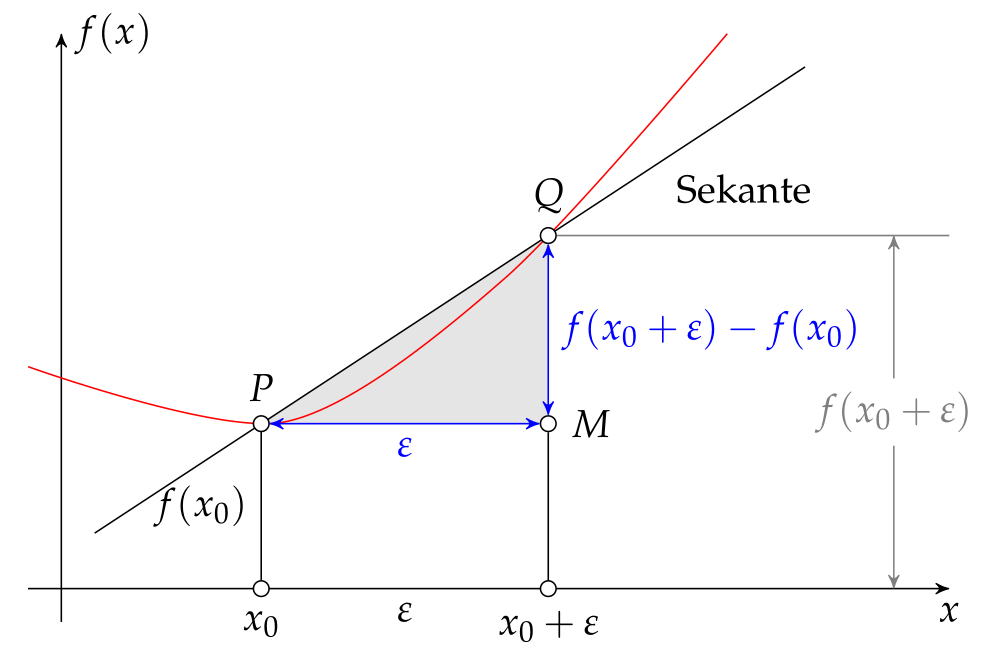
动画扩展
其实这个代码最好玩的地方并不在于上面的作图,而在于我们可以让这个图动起来,参见代码:
%!TEX program = pdflatex
\documentclass{article}
\usepackage{mathpazo}
\usepackage{tikz}
\usetikzlibrary{arrows,intersections}
\begin{document}
% 为了使用 Acrobat 删除外围区域,需要设置没有页码
\pagestyle{empty}
% TikZ 设定
\tikzset{thick,
> = stealth',
dot/.style = {draw,fill=white,circle,inner sep=0pt,minimum size=4pt}
}
\foreach \Q in {4,4.1,4.2,...,5,4.9,4.8,...,4.1} { %<-- added
\begin{tikzpicture}
% 画坐标系 并且定义了 O 、xmax 和 ymax
\coordinate (O) at (0,0);
\draw[->] (-0.3,0) -- (8,0) coordinate[label={below:$x$}] (xmax);
\draw[->] (0,-0.3) -- (0,5) coordinate[label={right:$f(x)$}] (ymax);
% 给出直线 x 与曲线 y 的路径
\path[name path=x] (0.3,0.5) -- (6.7,4.7);
\path[name path=y] plot[smooth] coordinates {(-0.3,2) (2,1.5) (\Q,2.8) (6,5)}; %<-- modified
% 利用 intersections 包的计算方法,得到了直线与曲线的交点坐标,分别命名为 i-1 和 i-2 (图中分别为 P 和 Q) 过点 P 的水平线与过 Q 的竖直延长线的交点标记为 M.
\begin{scope}[name intersections = {of= x and y,name = i}]
% 将PQ所形成的三角形区域(PQM)填充为灰色
\fill[gray!20] (i-1) -- (i-2 |- i-1) -- (i-2) -- cycle;
% 在空白处标记 Sekante
\draw (0.3,0.5) -- (6.7,4.7) node[pos=0.8,below right] {Sekante};
% 画出曲线路径 y,与之前代码几乎一样
\draw[red] plot[smooth] coordinates {(-0.3,2) (2,1.5) (\Q,2.8) (6,5)}; %<-- modified
% 从 P 向 x 轴引垂线,垂足坐标为 (i-1 |- O),标签为 x_0
\draw (i-1) node[dot,label={above:$P$}] (i-1) {} -- node[left] {$f(x_0)$} (i-1 |- O) node[dot,label={below:$x_0$}] {};
% Q 点向 M 引垂线
\path (i-2) node[dot,label={above:$Q$}] (i-2) {} -- (i-2 |- i-1) node[dot,label={right:$M$}] (i-12) {};
% M 向 x 轴引垂线,并且标注
\draw (i-12) -- (i-12 |- O) node[dot,label={below:$x_0 + \varepsilon$}] {};
% 连接 Q 与 M,并且标注
\draw[blue,<->] (i-2) -- node[right] {$f(x_0 + \varepsilon) - f(x_0)$} (i-12);
% 连接 P 与 M
\draw[blue,<->] (i-1) -- node[below] {$\varepsilon$} (i-12);
% x 轴上两个垂足之间标记
\path (i-1 |- O) -- node[below] {$\varepsilon$} (i-2 |- O);
% Q 的水平延长线
\draw[gray] (i-2) -- (i-2 -| xmax);
% 标注 Q 点的垂直距离,最精彩的是用到了 xshift=-0.5cm,简直赞!
\draw[gray,<->] ([xshift=-0.5cm]i-2 -| xmax) -- node[fill=white] {$f(x_0 + \varepsilon)$} ([xshift=-0.5cm]xmax);
\end{scope}
\end{tikzpicture}
\eject %<-- added
} %<-- added
\end{document}
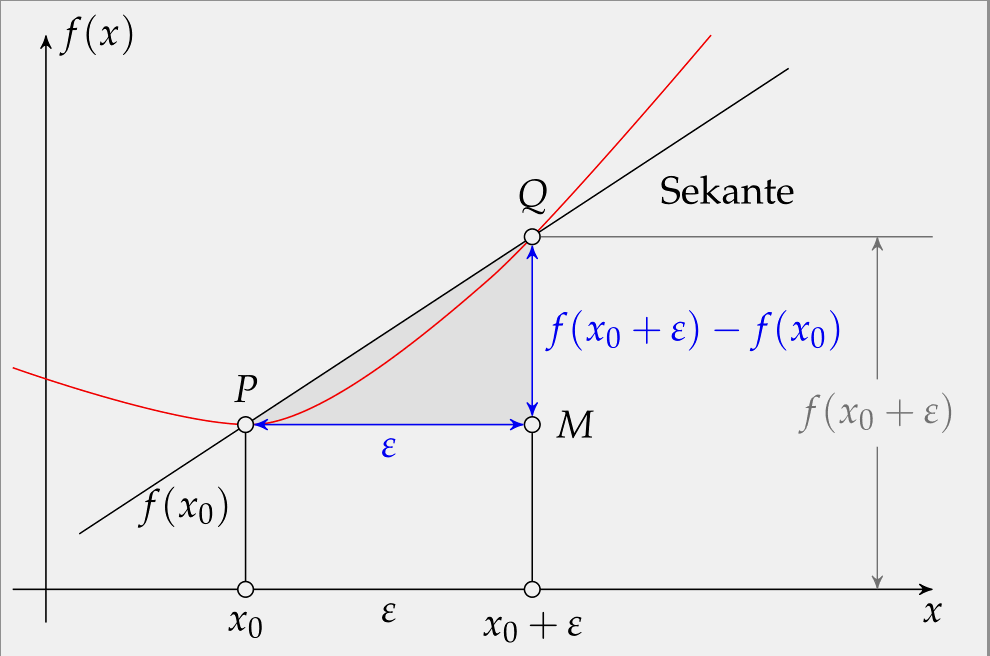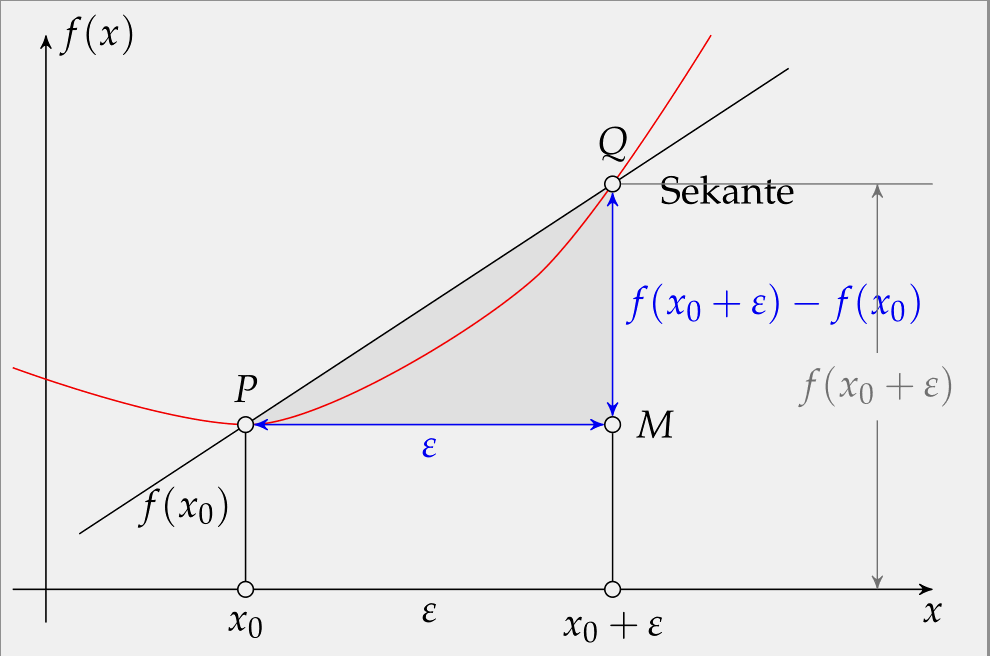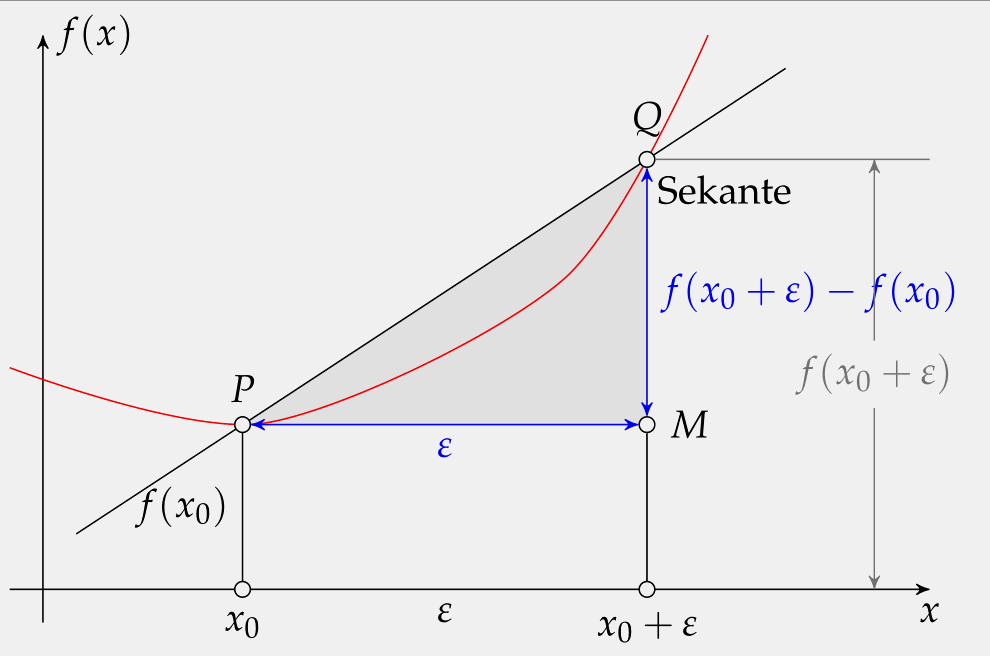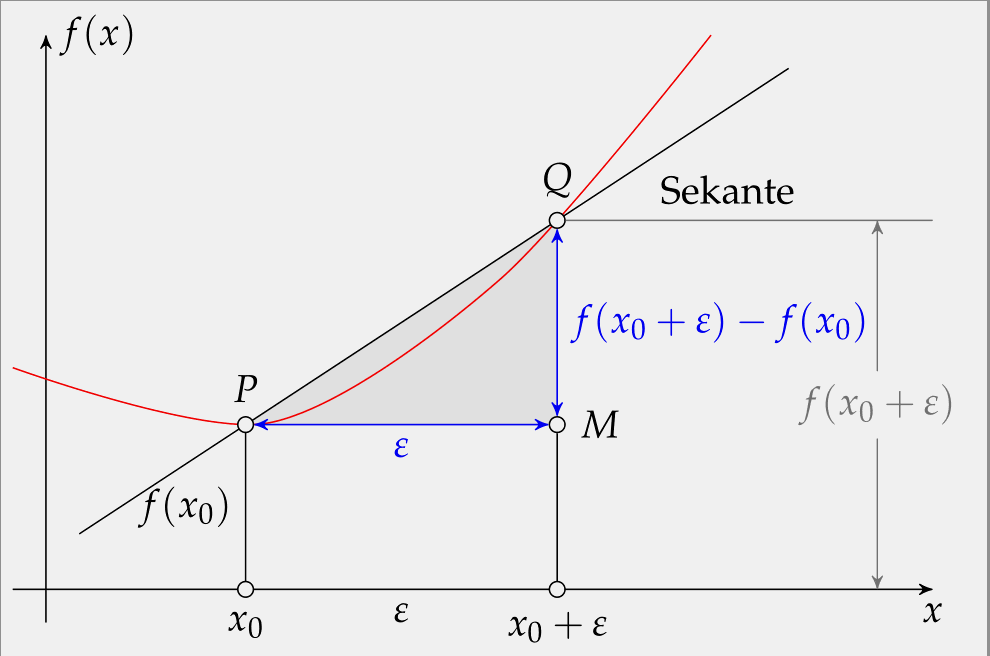
最后可以做成类似动画的效果,PDF下载地址:点击下载
下载之后的是 PDF 文件,用 Adobe Reader\Acrobat 打开,一页页翻,这是不是就是动画了,简直帅呆了!如果需要转成 GIF,原帖有转换的方法!Enjoy!
原帖地址:http://tex.stackexchange.com/questions/168297/plot-to-illustrate-secant-lines
选自:http://elegantlatex.tk/2014/05/07/tikz-derivative-process/




发表评论 取消回复